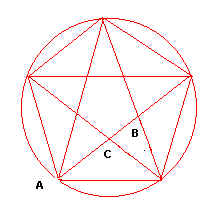
La sezione aurea fu studiata dai Pitagorici i quali scoprirono che il lato del decagono regolare inscritto in una circonferenza di raggio r è la sezione aurea del raggio e costruirono anche il pentagono regolare intrecciato o stellato, o stella a 5 punte che i Pitagorici chiamarono pentagramma e considerarono simbolo dell’armonia ed assunsero come loro segno di ricoscimento , ottenuto dal decagono regolare congiungendo un vertice si e uno no . A questa figura è stata attribuita per millenni à un’importanza misteriosa probabilmente per la sua proprietà di generare la sezione aurea , da cui è nata .

       Infatti i suoi lati si intersecano sempre secondo la sezione aurea :

   La Sezione Aurea, in quanto legge strutturale del corpo umano,ha conosciuto in Leonardo da Vinci (1452/1519) un geniale assertore , avendo collaborato con i suoi schizzi alla stesura del trattato "De Divina proportione" (Venezia,1509) di Luca Pacioli.

    A partire dal Rinascimento la Sectio Aurea acquista il crisma della bellezza estetica.  Secondo Luca Pacioli ed Albrecht  Dürer , la SectioAurea o numero d'Oro, era elemento proporzionale analogico tra la figura umana e la natura oggettiva. 

In campo filosofico, inoltre, l'Harmonia della Natura diviene causa e principio del mondo. Ci riferiamo agli scritti di G. Bruno " De la Causa, principio et Uno"(1584) oppure al "Mysterium magnum" ( 1623) di Jacob Böhme.  (***)

In botanica, fisica, zoologia, architettura, pittura e musica, oltre che in geometria in alcune relazioni riguardanti i poligoni regolari, la sezione aurea interviene in modo insistente. Essa, che non è altro che un semplice rapporto di numeri, si incontra ovunque, in natura, come nella scienza e nell'arte, e "contribuisce alla bellezza di tutto ciò che ci circonda."

L’equilibrio armonico che si percepisce nelle opere dell’arte classica e rinascimentale è il risultato di un’impostazione che si realizza in alcuni principi compositivi come l’utilizzo della sezione aurea. In realtà vari esperimenti suggeriscono che la percezione umana mostra una naturale preferenza per le proporzioni in accordo con la sezione aurea. Gli artisti, quindi, tenderebbero quasi inconsciamente a disporre gli elementi di una composizione in base a tali rapporti.

GEOMETRIA

La sezione aurea è il segmento medio proporzionale tra la lunghezza di tutto il segmento e la parte rimanente.
Ripartizione di un segmento in due parti, che stanno tra loro come la maggiore (a) sta al segmento intero (1); utilizzando i simboli si ha: 1:a=a:b.
a : x = x : (a - x) da cui  a(a - x) = x² da cui il valore positivo di x = = 0,618...

ARITMETICA

Il matematico pisano Leonardo Fibonacci fu ricordato soprattutto per via della sua sequenza divenuta ormai celeberrima. L’uso della sequenza di Fibonacci risale all’anno 1202. Essa si compone di una serie di numeri (0,1,1,2,3,5,8,13,21…).
Tra i numeri di questa successione esiste una relazione per cui ogni termine successivo è uguale alla somma dei due immediatamente precedenti. Più importante dal nostro punto di vista è però il fatto che il rapporto tra due termini successivi si avvicini molto rapidamente a 0,61:
1:2=0,500 8:13=0,615 
2:3=0,667 13:21=0,619
3:5=0,600 21:34=0,618
5:8=0,625 34:55=0,618
Sappiamo infatti che 0,618 è il rapporto della sezione aurea. Per altra via si giunge ad analoghe conclusioni. Se infatti dividiamo un segmento di lunghezza 1 in una parte maggiore x e in una parte minore 1-x tale che
(1-x) : x = x : 1  
poichè nelle proporzioni il prodotto dei termini estremi è uguale al prodotto dei medi:
x² = 1- x cioè x² + x - 1 = 0
possiamo ricavare il valore positivo di x 

x = + 0,618...

NATURA

In natura diversi tipi di conchiglie (ad esempio quella del Nautilus) hanno una forma a spirale fatta secondo i numeri di Fibonacci.

In botanica, la disposizione a frattali degli elementi che compongono le foglie degli alberi, seguono un diagramma logaritmico analogo ai suoni emessi da un monocordo. A dimostrazione di tale tesi, lo studioso svizzero Hans Kayser pubblicò , nel 1943, un testo di ben 324 pagine per comprovare l'esattezza di tale affermazione, sia dal punto di vista culturale che matematico. Sebbene l'universo frattale sia stato scoperto in chiave moderna da Benoit B. Mandelbrot, nel 1975, la sua storia appartiene alle conoscenze esoteriche dell'antico Egitto e pertanto, alla filosofia orfica e pitagorica. (...) Già dai tempi arcaici dell'antico Egitto, infatti , si assumeva l'organicismo della Natura  e le sue leggi numeriche come fattori essenziali che preesistono a tutti gli eventi, i quali seguono sempre il medesimo divenire.(***)

VISITATE LA GALLERIA FOTOGRAFICA 

SULLA SECTIOAUREA IN NATURA

ARTE

  Non ci deve certo stupire se l'uomo, consapevolmente o no, riveli una certa propensione per l'utilizzazione della sezione aurea, che applica nella sua produzione artistica.

(***)  Nell'arte figurativa e nell'architettura. i concetto di Harmonia e delle sue leggi numeriche hanno governato fin dalle civiltà arcaiche sia attraverso la Sezione aurea. sia attraverso i processi di concrescimento di tipo spiralico, meglio conosciuti come serie di Fibonacci.

 Cosiffatte proporzioni sono la base delle piramidi egizie, come del tempio greco, del duomo romano e delle cattedrali gotiche. (***)

  Tra i primi utilizzatori di questo rapporto ci furono sicura mente i Greci. 

 In un'anfora greca (IV-III secolo a.C.) il diametro maggiore sta al diametro del collo come 1:0,618; il listello all'altezza dei manici divide l'altezza totale in una proporzione aurea, che si riduce anche nel rapporto tra la fascia decorata a figure e la parte superiore del vaso. 
Anche nell'architettura la sezione aurea è stata applicata sin dai tempi più antichi. Il rapporto tra lunghezza e larghezza nei templi greci era di preferenza 1:0,618 e il timpano era costruito come un triangolo isoscele avente un angolo al vertice di 108°.

La sezione aurea è anche stata usata ampliamente in pittura, in molti quadri, soprattutto dal Rinascimento, questa proporzione veniva usata moltissime volte all'interno dell'opera. Si dice, ad esempio, che nella rappresentazione di un panorama l'orizzonte deve dividere l'altezza del quadro secondo la sezione aurea per ottenere un risultato più soddisfacente.

LETTERATURA CONTEMPORANEA

Leggete il paragrafo sulla Sezione Aurea dall'avvincente thriller  di Dan Brown "IL CODICE DA VINCI" pubblicato in Italia da A. Mondadori editore, traduzione di Riccardo Valla

VISITATE LA GALLERIA FOTOGRAFICA 

SULLA SECTIOAUREA IN PITTURA SCULTURA ARCHITETTURA 

LINK

ASTRONOMIA

Tutti i pianeti interni distano dal Sole nelle proporzioni della successione (Sole 1, Mercurio 1, Venere 2, Terra 3, Marte 5); e quelli esterni distano ugualmente da Giove (Giove 1, Saturno 1, Urano 2, Nettuno 3, Plutone 5); mentre la distanza fra Marte e Giove (confini dei due blocchi) è pari ad un decimo di quella fra il Sole ed il decimo e ultimo più importante corpo astrale del Sistema Solare: Plutone. Il perché di tutto questo è tuttora indimostrato, non potendo certo esser frutto di stocastica cosmica.

MUSICA

      Leonardo Pisano, detto Fibonacci (1175/1240) fece parte della cerchia dei dotti che gravitava attorno a alla corte di Federico II di Svevia.

   Egli introdusse in Europa i numeri e la matematica araba.

Nella successione da lui inventata e che porta il suo nome , ogni termine si ottiene dalla somma dei due precedenti. I primi elementi sono pertanto:

1,1,2,3,5,8,13,21,34,55,89,144

A partire da tale successione, se ne forma una di tipo frazionario, dalla quale emergono i seguenti rapporti:

1/1;  2/1; 3/2;  5/3;  8/5;  13/8;  21/13;  34/21;  55/34,  89/55;  144/89 ecc.    

i cui valori decimali approssimati sono:

1; 2; 1,5; 1, 666;  1,6;  1,625;  1,615;  1, 619;  1, 617;  1, 6181; 1, 6180 ecc. 

che corrispondono agli intervalli musicali:

unisono=1

ottava=2

quinta=1,5

sesta maggiore=1,666

sesta minore=1,6

in cui gli ultimi sono complementari degli intervalli di terza minore e maggiore.

se poi applichiamo la serie di Fibonacci alle sovrarmoniche e alle sottoarmoniche di un suono di riferimento(ad es. il DO) avremo che i numeri in successione aurea 3,5,e 8 superiori al suono dato corrispondono ai suoni MI, SOL e Do acuto e i numeri 3, 5 e 8 inferiori allo stesso suono corrispondono al LAb, FA e DO grave . Abbiamo quindi l'harmonia maggiore e minore.  (***)

Le distanze do-re, re-mi, fa-sol, sol-la, la-si sono ognuna un tono, mentre le distanze mi-fa e si-do sono un semitono. Raggruppando il numero di vibrazioni dei dodici semitoni che si susseguono ricaviamo una proporzione continua:
T1:T2=T2:T3=T3:T4 eccetera
Possiamo arrivare a dire che il numero delle variazioni che si differenziano per otto semitoni si comporta quindi come la sezione aurea:
T1:T9=T9:T17=1:1,618
Da ciò deriva che anche negli organi di corti dell'apparato uditivo umano, cui compete la selezione dei suoni, si deve poter riscontrare il principio della sezione aurea; non solo, ma essa è anche punto di riferimento nella costruzione di canne di organo e altri strumenti musicali. Possiamo anche ipotizzare che negli organi di Corti dell'apparato uditivo umano, che reagiscono alle tonalità pure, operi il principio dei numeri della successione di Fibonacci. In un violino, il cui timbro dipende dalle dalle possibilità di vibrazione di tutte le parti, la sezione aurea gioca sicuramente un ruolo; in effetti se misuriamo uno Stradivari vediamo che esso è contenibile entro quattro pentagoni regolari i cui lati fungono da tangenti, determinando una linea estremamente armoniosa.

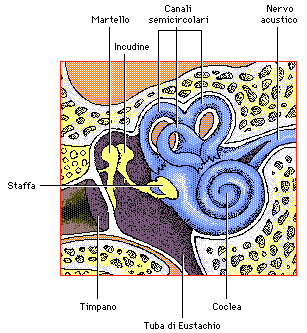
 (***) La strutturazione a nautilus della coclea dell'orecchio umano , situata alla fine dell'orecchio interno segue le leggi della sezione aurea, per cui si può ben dire che : " l'orecchio è stato creato dal suono, come l'occhio dalla luce" (***)

Bibliografia 

(***) i paragrafi contenuti tra due (***) sono stati tratti dal volume di Emiliano Albani e Diego Pierpaoli " MUSICA AD FIGURAS" edizione del Museo di arte Immanente di Arquata del Tronto (AP), l'articolo sulla sezione aurea è di Alessio di Benedetto . Pagg. 34/37.